- Registrado
- 30 July 2019
- Mensajes
- 1.860
- Puntos de reacción
- 3.051
- Puntos
- 349
- Edad
- 24
- Ubicación
- Sevilla, España
- Puntos
- 1.610
Un saludo a los lectores que se tomen la molestia de revisar esta sección del foro. Guarden interés en este post, pues puede interesaros este campo tanto como a mí, donde podréis extraer de aquí las nociones fundamentales de uno de los siete grandes problemas de las Matemáticas. Toda la información base que queráis consultar la tenéis en Wikipedia (https://es.wikipedia.org/wiki/Hipótesis_de_Riemann), o cualquier otra plataforma oficial. Llevo investigando este tópico durante más de cinco años, y aunque sea joven, las ganas son tremendas. Las capturas al final de este post pertenecen al artículo de investigación que llevo realizando desde hace dos años, el cual quedará publicado en el dominio privado del Instituto Clay de Matemáticas una vez terminado las proposiciones iniciales del problema (solo comparto las dos primeras páginas de las casi doscientas de momento, pues se trata de una investigación privada).
Durante más de ciento cincuenta años, la comunidad matemática ha trabajado y extrapolado numerosos teoremas útiles en áreas como Topología y Análisis. El objeto de estudio de este problema casi imposible es demostrar el comportamiento de una función que valora en el plano de los números imaginarios, con el fin de identificar un patrón en sus raíces (esto es, ζ(s)=0). La dificultad de exponer condiciones e hipótesis para concluir en resultados dignos de comentario y análisis (valga la redundancia), es analizar concienzudamente definiciones alternativas a la función original, denominado más precisamente como extensión analítica.
Hay una gran variedad de conjeturas en órbita a esta cuestión, pues el problema parece haberse resuelto recientemente, pero la demostración queda invalidada por tratarse de una simplificación masiva del problema de partida. En este intento personal de alcanzar resultados antes nunca vistos, dispongo de programas y gráficos que facilitarán el estudio puntual y uniforme de espacios conexos a través de las definiciones de la función antes definida. Teniendo en cuenta que estoy solo en el intento de dar pasos más allá que nadie, en plena cuarentena, me hace pensar que no soy el único matemático (o estudiante) que opta afrontar sus conocimientos y avanzar en el campo que les interese. Os animo a compartir en este post vuestras ideas y sugerencias, al igual que cualquier duda que recurra a vuestras mentes.

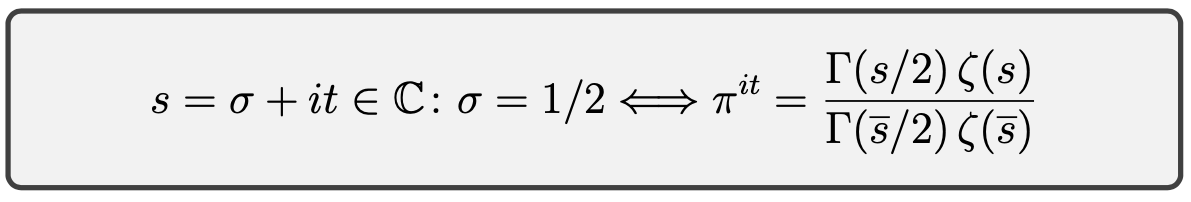

Un saludo.
Daniel Dmitrienco Herrera.
Durante más de ciento cincuenta años, la comunidad matemática ha trabajado y extrapolado numerosos teoremas útiles en áreas como Topología y Análisis. El objeto de estudio de este problema casi imposible es demostrar el comportamiento de una función que valora en el plano de los números imaginarios, con el fin de identificar un patrón en sus raíces (esto es, ζ(s)=0). La dificultad de exponer condiciones e hipótesis para concluir en resultados dignos de comentario y análisis (valga la redundancia), es analizar concienzudamente definiciones alternativas a la función original, denominado más precisamente como extensión analítica.
Hay una gran variedad de conjeturas en órbita a esta cuestión, pues el problema parece haberse resuelto recientemente, pero la demostración queda invalidada por tratarse de una simplificación masiva del problema de partida. En este intento personal de alcanzar resultados antes nunca vistos, dispongo de programas y gráficos que facilitarán el estudio puntual y uniforme de espacios conexos a través de las definiciones de la función antes definida. Teniendo en cuenta que estoy solo en el intento de dar pasos más allá que nadie, en plena cuarentena, me hace pensar que no soy el único matemático (o estudiante) que opta afrontar sus conocimientos y avanzar en el campo que les interese. Os animo a compartir en este post vuestras ideas y sugerencias, al igual que cualquier duda que recurra a vuestras mentes.
Un saludo.
Daniel Dmitrienco Herrera.
